I’ve been working on an Android game for the past few months and at one point I needed to detect if a point (P) fell within the confines of an arc. I was surprised to find that Android’s API’s didn’t have anything to support this. After some Googling I still couldn’t find anything so I figured I’d post how I do it (partially in the hope that someone else might present a faster way ;)).
First, lets look at our arc:
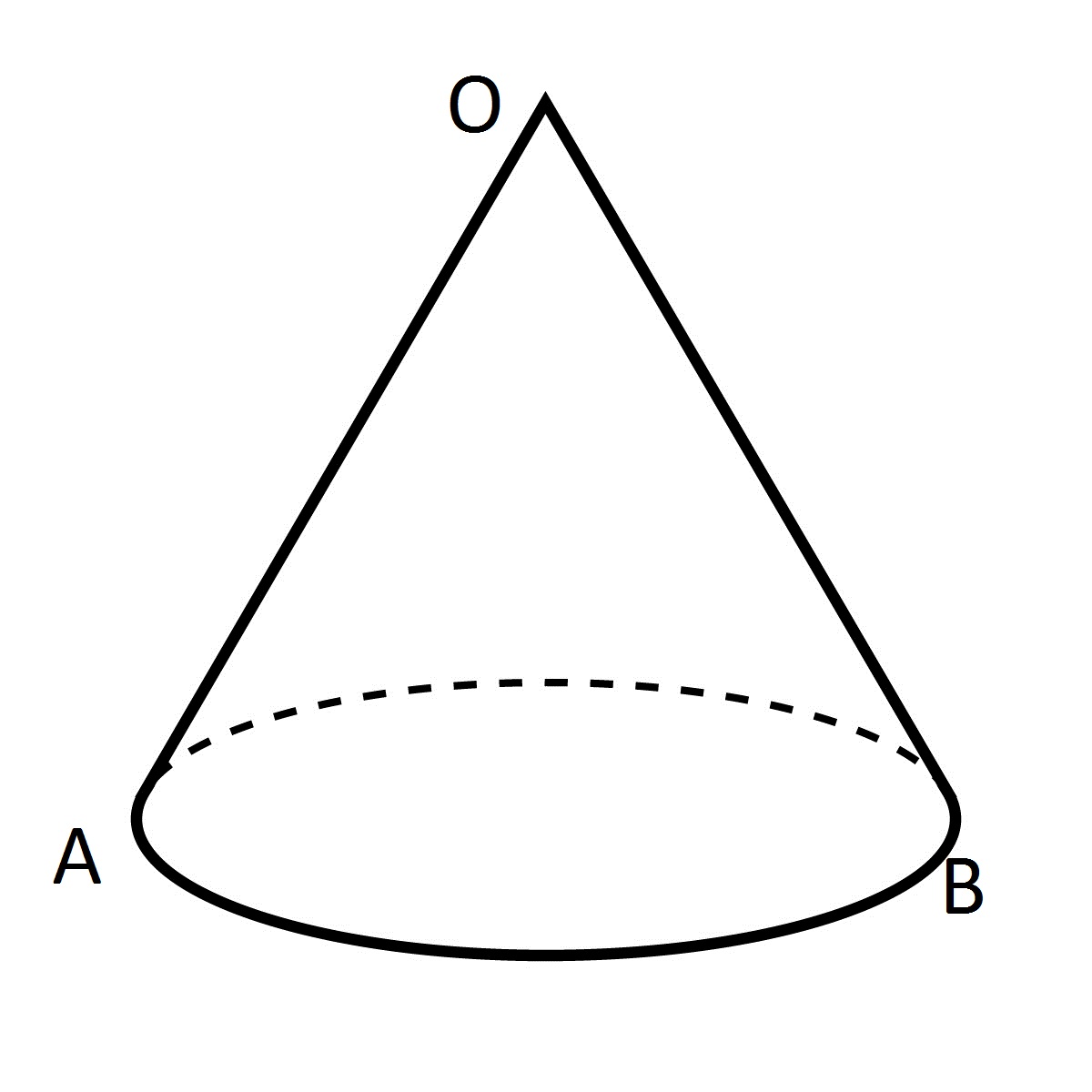
You can see that in my representation I actually have a cone (2d, not 3d) and I need to detect collision in the cone. So, not only do I need to check if the P falls on the arc, but also if it is within the cone. This means I have to things to check:
- Distance from start of cone (O) to end of arc
- If P is between the start and end of the arc (A and B)
Range Check
Well, the distance part is rather easy, since I know position A and I know position O, I know the radius. Now I just need to remember that an arc in my case is just a part of a uniform circle so the distance is really just the radius (r) of the circle. Basic math here:
- Known Diameter: r = D / 2
- Known Circumferance: r = C / (2 * PI)
So now, if P is > 0 and P <= r, I know that P is in range.
Arc Collision
Next comes the check to see if P is between A and B. For this we again need to remember that the arc is really just a slice of a circle. So, the first thing we need to determine is the degree at which P is from O (lets call it dP).
- Take the position of O
- Take the position of P
- Use Math.atan(P.y-O.y, P.x-O.x) (please note that I’m using a GFX library for this part, so this may not be 100% correct as I haven’t tested it)
Now we know where P actually falls, degree wise, in relation to O. All we have to test now is if P is between A and B. But, that’s not as easy as you think. Sure, if A = 5 and B = 20 and dP = 10, we know it is in between. What happens when A = 320 (remember that a circle goes to 360), B = 20, and dP = 10? Well, the A < dP would fail because A > dP but for us, dP is still inside the arc.
This is what I came up with and, to be honest, where I’m hoping someone can tell me a better way (if there is one):
if (((B < A) && ((A <= dP && dP < 360) || (dP <= B && dP >= 0)))
|| ( A <= dP && dP <= B))
{
return true;
}
return false;
Basically, if B < A that means that B has crossed over the 360/0 point of the circle since A is greater that B. If this has occurred then check if A <= dP while dP < 360 OR check if dP <= B while dP >= 0. This covers any issues around the 360/0 point on the circle. If we don’t have the 360/0 point issue its just a simple compare of A <= dP and dP < B.
You now know if P is within your cone!

2 Responses to Arc Collision